Bài 2: Kỹ Năng Lập trình Matlab

Nội dung
1. Lập trình hàm
2. Các cấu trúc điều khiển trong lập trình MATLAB
3. Vẽ đồ thị đường
4. Vẽ đồ thị các hình và mặt 3D
5. Các chú ý khi lập trình MATLAB
1. Lập trình hàm
Hàm do người dùng tự định nghĩa: khá giống với scripts, chỉ khác ở việc cần phải định nghĩa hàm.
Một số chú ý về khai báo hàm:

Không cần từ khóa return để trả về giá trị. MATLAB sẽ tự trả về biến có tên trùng với biến đã được khai báo từ hàm.

Các biến được định nghĩa trong phạm vi hàm nếu không được trả lại sau lời gọi hàm đều sẽ không được MATLAB lưu lại.

Nạp chồng hàm trong MATLAB:

- Việc nạp chồng hàm được hiểu đơn giản là các hàm có cùng tên nhưng có nhiều cách đưa tham số vào khác nhau, cách nhận được tham số ra cũng khác nhau.

- Trong MATLAB, hầu hết các hàm built-in đều được nạp chồng. 

Ví dụ: a = zeros(2,2) ; zero(2,3,4) % Tạo ma trận không kích cỡ nào cũng có thể thực hiện được với lệnh zeros

d = size(a); [m,n] = size(a) ; m2 = size(a, 2)

- Để biết được tính năng của các hàm, luôn cần dùng lệnh help

Nếu muốn, bạn cũng có thể nạp chồng hàm bạn viết bằng cách dùng các biến đặc biệt cho biết lượng biến vào và ra ( tham khảo varargin,varargout, nargin, nargout)

Bài tập 1:

1. Viết 1 hàm có phần định nghĩa như sau:

function plotSin(f1) % Hàm không có tham số đầu ra, chỉ có tham số đầu vào là f1

2. Hàm có nhiệm vụ vẽ một hình sin với tần số f1, trong khoảng [0, 2*pi] (sử dụng 16 điểm trong 1 chu kỳ để vẽ hình).
Thực hiện: mở một mfile mới, save as plotSin.m, đánh các dòng sau:

function plotSin(f1)
x = linspace(0,2*pi,f1*16+1)
figure
plot(x,sin(f1*x))

Bài tập 2:

1. Khai báo hàm tính diện tích hình chữ nhật như sau:

function s = squareArea(width, length) % Hàm có 2 tham số vào là chiều dài và chiều rộng, trả về giá trị diện tích hình chữ nhật
2. Viết lệnh để hàm tính diện tích của hình chữ nhật có 2 kích thước là 2 tham số đầu vào.

2. Các cấu trúc điều khiển trong lập trình MATLAB

Các toán tử quan hệ: các phép toán logic được cho trong hình vẽ dưới đây

Các giá trị logic Boolean: 0 : false, 1 : true

a/ Cấu trúc rẽ nhánh: if/ else/ elseif

Đây là cấu trúc cơ bản trong mọi ngôn ngữ lập trình, MATLAB có một chút khác biệt ở từ khóa elseif

Chú ý: Các câu lệnh nằm giữa if-end, if-else-end, ... không cần có dấu ngoặc.

b/ Cấu trúc lặp

Vòng lặp For: sử dụng khi biết số lần cần lặp

Biến lặp (loop variable):

được định nghĩa như một vector

trong vòng lặp thì có giá trị là một số, chỉ số vòng lặp hiện tại

không nhất định là các giá trị liên tiếp, nhưng thông thường nên để là các giá trị liên tiếp

Các câu lệnh trong vòng lặp: mọi câu lệnh nằm giữa hai từ khóa for - end.

Vòng lặp while: tổng quát hơn vòng lăp for, có thể dùng khi chưa biết số lượng vòng lặp

Các lệnh giữa hai từ khóa while và end sẽ được thực hiện chừng nào điều kiện lặp còn đúng

Cần chú ý tránh vòng lặp vô hạn!

Bài tập 1:

1. Thay đổi hàm plotSin(f1) ở trang trước để hàm nhận 2 đầu vào: plotSin(f1,f2)

2. Nếu như số lượng biến vào là 1, thực hiện lệnh plot vẽ đồ thị hàm như trong bài trước, ngược lại thì đưa ra dòng chữ: 'Two inputs were given' (Gợi ý: số lượng biến vào là 1 hàm được MATLAB định nghĩa sẵn: nargin)

Thực hiện:
function plotSin(f1,f2)
x = linspace (0, 2*pi, f1*16+1);
figure
if nargin ==1
         plot(x, sin(f1*x));
elseif nargin ==2
         disp('Two inputs were given');
end

Bài tập 2: 

1. Khai báo hàm: function check = checkTriangular(x1, x2, x3)

2. Hàm có nhiệm vụ kiểm tra ba kích thước được cho có tạo thành một tam giác được hay không. Nếu có thể, trả về giá trị 1, ngược lại trả về giá trị 0.

3. Khai báo hàm: function area = areaTriangular(x1, x2, x3). Hàm có nhiệm vụ kiểm tra xem liệu x1, x2, x3 có tạo thành 1 tam giác không rồi tính diện tích tam giác tạo thành nếu có thể. Nếu không tạo thành được tam giác thì trả về giá trị -1. (trong hàm areaTriangular hãy gọi hàm checkTriangular ở trên để kiểm tra)

3. Vẽ đồ thị đường

Các tùy chọn (option) của lệnh plot

Khi dùng lệnh plot, có thể lựa chọn màu của đồ thị (color), hình để đánh dấu điểm trên đồ thị (mark), kiểu đường (line style) bằng cách thêm vào một số từ như sau:

Có thể vẽ các điểm mà không nối các điểm đó với nhau bởi các đường bằng câu lệnh như sau: >> plot(x,y,'.')

Để biết được tất cả các màu sắc, kiểu đánh dấu, kiểu đường mà MATLAB hỗ trợ, bạn hãy dùng câu lệnh: >> help plot

Để tọa chú thích cho các trục tọa độ, hay tên của đồ thị dùng lệnh xlabel, ylabel, title. Ví dụ:
>> x=1:0.1:5;
>> y=sin(x)+x/2;
>> figure
>> plot(y,x)
>> xlabel('time)
>> ylabel('f(x)')
>> title('Do thi ham so y = f(x)')

Có thể thay đổi các lựa chọn ngay trên màn hình figure đã vẽ

Vẽ đồ thị trên hệ tọa độ vuông góc

Để minh họa cách vẽ đồ thị trên hệ tọa độ Đề Các, các bạn hãy gõ ví dụ sau: 

>> x = -pi:pi/100:pi;
>> y = cos(4*x).*sin(10*x).*exp(-abs(x));
>> plot (x,y, 'k-');
Tọa độ loga thường dùng khi vẽ đồ thị Bode. Để vẽ đồ thị trên tọa độ semilog hay tọa độ loglog, sử dụng các câu lệnh như sau:
>> semilogx(x,y,'k');
>> semilogy(y,'r.-');
>> loglog (x,y);
Ví dụ: 

>> x = 0:100;
>> semilogy(x, exp(x), 'k.-');
Vẽ đường 3D
Với MATLAB, việc vẽ đường trong không gian 3 chiều cũng rất đơn giản. Ví dụ để vẽ đường xoắn ốc:
>> time = 0:0.0001:4*pi;
>> x = sin(time);
>> y = cos(time);
>> z = time;
>> plot3(x,y,z, 'k', 'LineWidth',2);
>> zlabel('Time');

Để giới hạn các trục x, y, z, dùng các lệnh xlim, ylim, zlim

Để xem rõ hơn, có thể xoay đồ thị 3D thu được trong màn hình figure.

Một số hàm hỗ trợ sẵn để tùy chỉnh đồ thị:
>> axis square % Làm cho đồ thị có các trục tạo thành hình vuông
>> axis tight % Làm cho đồ thị vừa với đồ thị được vẽ
>> axis equal % Làm cho 2 trục x, y cùng co/giãn với một tỉ lệ
>> axis xy % Làm cho 2 trục nhận điểm ở góc dưới bên trái làm gốc
>> axis ij % Làm cho 2 trục nhận điểm ở góc trên bên trái làm gốc

Để vẽ nhiều đồ thị trên một figure, ta dùng lệnh subplot

>> x = 0:0.1:10;
>> subplot(2, 3, 1) %Chia màn hình figure thành sáu đồ thị với hai hàng, ba cột.
% Đồ thị được vẽ lúc này sẽ ở vị trí số 1, tức là hàng 1, cột 1
>> plot(x,x-5) % Đồ thị này sẽ ở vị trí hàng 1, cột 1.
>> title ('Đồ thị hàm số y = x - 5');% Mỗi đồ thị được vẽ có thể có tên đồ thị, tên trục riêng.
>> subplot(2, 3, 2) % Lúc này đồ thị được vẽ tiếp theo sẽ ở vị trí số 2, tức là ở hàng 1, cột 2.
>> plot (x, sin(x), 'k')
>> title('Đồ thị hàm số y = sin(x)');
>> subplot (2, 3, 4:6) % Gộp các vị trí từ 4 đến 6 lại để vẽ đồ thị tiếp theo
>> plot (x, exp(x), 'r')

Để đóng màn hình figure:
 >> close([1 3]) % Đóng figure 1 và 3

>> close all % Đóng tất cả các figure đang có (thường dùng khi lập trình các script/ function)

Copy/ Paste Figure 

Các Figure có thể được copy/ paste sang các chương trình ứng dụng khác (MS Word, Power Point, Paint ...)

Trên màn hình figure, chọn Edit/Copy Options/ Figure copy template để chọn các thuộc tính của ảnh trước khi copy. Sau đó chọn Edit/ Copy Figure để Copy đồ thị ra các chương trình khác. 

Save đồ thị

Các figure có thể được save lại theo mọi định dạng: 

.fig (dạng dữ liệu ảnh của MATLAB, là dạng không bị mất một dữ liệu nào của bức ảnh, tuy nhiên không xem được bởi các trình xem ảnh thông thường) 

.bmp ảnh không nén

.eps ảnh theo tỉ lệ với chất lượng cao 

.pdf ảnh được nén lại, mở với phần mềm đọc pdf

. jpg, .jpeg dạng file ảnh né.
4. Vẽ hình và mặt cong 3D
Vẽ các mặt cong 3D
- Ví dụ: Vẽ mặt cong f (x, y) = sin(x)cos(y), với x thuộc [-pi, pi]; y thuộc [-pi, pi]
- Sử dụng lệnh surf : dựng một lưới tọa độ gồm 2 phần tử x, y, kết hợp với độ cao z để xác định được các điểm trên mặt cong, sau đó nối các điểm đó tạo thành 1 mặt.
- Để tạo ma trận tính các tọa độ z có thể làm 1 trong 2 cách:
      dùng vòng lặp: cách này tốn thời gian và công sức, ít dùng
      dùng hàm build-in: meshgrid 

      >> x = -pi:0.1:pi; % Tạo các vector x, y
      >> y = -pi:0.1:pi;
      >>[X,Y] = meshgrid(x,y); % Tạo lưới tọa độ [X,Y]
      >> Z = sin(X).*cos(Y); % Tạo tọa độ Z
      >> surf(X,Y,Z) % Vẽ mặt cong. Kết quả như sau:

Giống như lệnh plot, lệnh surf có những tùy chỉnh, bạn hãy thử đánh các lệnh sau để xem hiệu quả của chúng
>> shading faceted
>> shading flat
>> shading interp
>> colormap(gray)
Để vẽ đồ thị các đường đồng mức 2 chiều, sử dụng lệnh contour
>> contour (X,Y,Z, 'LineWidth', 2)
% Lệnh này sử dụng các tham số giống như lệnh surf
% Màu sắc trên đồ thị thu được sẽ thể hiện cao độ khác nhau
% Tùy chỉnh 'LineWidth' giúp thay đổi độ dày của nét vẽ
% Với lệnh này, bạn cũng có thể thay đổi cách đánh màu
>> hold on % Giữ đồ thị đang có và vẽ tiếp đồ thị tiếp theo vào cùng 1 figure
>> mesh(X,Y,Z)
Bài tập
Sửa lại hàm plotSin để thực hiện việc sau:
1. Nếu đầu vào là 2 tham số, tính hàm sau:
Z = sin(f1*x) + sin(f2*y)
với y tính giống x, chỉ khác là f1 thay bởi f2 (gợi ý: dùng meshgrid để tính X, Y => tính Z)
2. Chia đồ thị thành 2 phần, phần trên vẽ các đường đồng mức của đồ thị dùng lênh contour. Phần dưới vẽ mặt cong với lệnh surf.
Hướng dẫn: sửa hàm plotSin như sau:
function plotSin(f1,f2)
x = linspace(0,2*pi,round(16*f1)+1);
figure
if nargin == 1
plot(x,sin(f1*x)),'rs--','LineWidth',2,'MarkerFaceColor','k');
elseif nargin == 2
y = linspace(0, 2*pi, round(16*f2) +1);
[X, Y] = meshgrid(x, y);
Z = sin(f1*X)+sin(f2*Y);
subplot(2,1,1);
contour(X,Y,Z,'LineWidth',2);
subplot(2,1,2);
surf(X, Y, Z);
end
MATLAB hỗ trợ nhiều loại đồ thị
đặc biệt khác đồ thị tọa độ cực: lệnh polar . Ví dụ
>> polar(0:0.01:2*pi,cos((0:0.01:2*pi)*2))
biểu đồ dạng cột, lệnh bar . Ví dụ
>> bar(1:10, rand(1,10));
lệnh quiver - để vẽ thêm đạo hàm trên đồ thị
>> [X, Y] = meshgrid(1:10, 1:10);
>> quiver(X,Y,rand(10), rand(10);
lệnh stair - để vẽ các hàm hằng rời rạc
>>stairs(1:10, rand(1,10));
lệnh fill - vẽ và tô màu một hình đa giác
>> fill([0 1 0.5], [0 0 1], 'r');
Để biết rõ hơn về các loại đồ thị, sử dụng lệnh help hoặc gõ >> doc specgraph để xem toàn bộ các loại đồ thị được hỗ trợ.
5. Một số chú ý khi lập trình

• Hàm find là một hàm rất quan trọng khi lập trình với MATLAB
• giúp tối giản các dòng code và tránh được các vòng lặp trong chương trình
• có thể giúp tìm kiếm chỉ số của các phần tử thỏa mãn điều kiện phức tạp
• Cách dùng cơ bản: index = find (điều kiện) . ví dụ:
• >> x = rand (1, 100);
• inds = find (x>0.4 & x<0 .6="" span="">
• %inds sẽ chứa các chỉ số của vector x mà có giá trị nằm giữa 0.4 và 0.6. Câu lệnh đó thực hiện qua các bước:
• % x>0.4 : trả lại 1 vector mà các số thỏa mãn điều kiện này là 1, còn không thỏa mãn là 0.
• % x<0 .6="" :="" c="" l="" n="" ng="" nh="" span="" t="" tr="" u="">
• % Toán tử & : tổng hợp 2 kết quả ở trên theo luật logic 1&1 =1, 1&0=0&0=0&1 = 0.
• % Cuối cùng lệnh find sẽ trả về các chỉ số được đánh số 1.
• Tối ưu hóa mã nguồn: để tối ưu hóa mã nguồn, đòi hỏi bạn tuân theo một số nguyên tắc lập trình nhất định với MATLAB và thực tập lập trình liên tục trong một thời gian dài. Một số nguyên tắc được nêu ra như sau:

1. Nguyên tắc về đặt tên (cho việc lập trình nói chung)

    - Việc đặt tên biến, tên hàm theo một nguyên tắc giúp bạn lập trình hoặc đọc chương trình của mình và của người khác một cách nhất quán,  rõ ràng, nhanh chóng hơn. 

    Đặt tên theo quy tắc sau:

    + tên lớp (class) : Viết hoa chữ cái đầu tiên trong từ. Ví dụ: ConNguoi, DoThi

    + tên hàm, scripts : bắt đầu bằng chữ thường còn lại giống class. Ví dụ: plotSin, veDoThi

    + hằng số: tất cả viết hoa

    + nên đặt tên gợi nhớ, không quá dài, quá ngắn; tránh mập mờ 

     2.  Tránh các vòng lặp không cần thiết khi lập trình MATLAB

    - Khi lập trình với MATLAB, để tăng tốc độ thực hiện chương trình, bạn luôn nhớ rằng hầu như các hàm build-in của MATLAB đều chạy nhanh hơn các đoạn code mà chúng ta viết với cùng chức năng sử dụng. Những người phát triển MATLAB đã hoàn thiện mã nguồn của họ và dịch trước các lệnh build-in.We should not reinvent the wheel!

    - Vì vậy nên tập sử dụng các hàm được định nghĩa sẵn, nó giúp chương trình ngắn hơn, chạy nhanh hơn.

Ví dụ 1: Cho mảng a, tìm mảng b sao cho mỗi phần tử của b bằng tổng hai phần tử liên tiếp của mảng a. tức là:

        b(n) = a(n) + a(n-1) với n>1

        b(1) = a(1)

Cách làm thứ 1: dùng vòng lặp, giống như lập trình C/C++ hay Java

a = rand(1,100);
b=zeros(1,100);
for n=1:100
     if n==1
            b(n) = a(n);
     else
            b(n) = a(n-1) + a(n);
     end
end

Cách làm thứ 2: dùng các build-in của MATLAB

                a = rand(1,100);

                b = [0 a(1:end-1)] + a;

Rõ ràng cách làm thứ 2 vừa nhanh vừa đỡ phức tạp hơn.

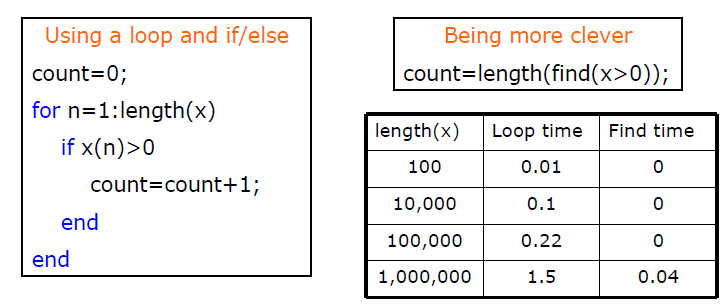
Ví dụ 2 sẽ cho thấy khả năng của lệnh find. Tìm các phần tử dương của mảng x, với x = sin(linspace(0,10*pi,100))